Graphs can be represented in various ways in Java, with each representation offering specific advantages depending on the operations you need to perform on the graph.
There are two ways to store Graphs into the computer’s memory:
- Sequential representation
- Linked list representation
Sequential Representation
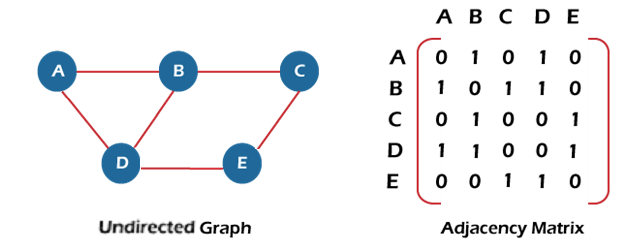
- Sequential representation, also known as an adjacency matrix, is a way to represent a graph using a two-dimensional array.
- It’s called sequential because the edges are stored in a sequential manner. Here’s an example of a sequential representation in Java:
- If adj[i][j] = w, it means that there is an edge exists from vertex i to vertex j with weight w.
- An entry Aij in the adjacency matrix representation of an undirected graph G will be 1 if an edge exists between Vi and Vj. If an Undirected Graph G consists of n vertices, then the adjacency matrix for that graph is n x n, and the matrix A = [aij] can be defined as –
- aij = 1 {if there is a path exists from Vi to Vj}
- aij = 0 {Otherwise}
- It means that, in an adjacency matrix, 0 represents that there is no association exists between the nodes, whereas 1 represents the existence of a path between two edges.
class Graph {
private int[][] adjacencyMatrix;
private int numVertices;
// Constructor
public Graph(int numVertices) {
this.numVertices = numVertices;
this.adjacencyMatrix =
new int[numVertices][numVertices];
}
// Function to add an edge between two vertices
public void addEdge(int i, int j, int weight) {
// Assuming a simple graph without self-loops
adjacencyMatrix[i][j] = weight;
adjacencyMatrix[j][i] = weight;
}
// Print the adjacency matrix
public void printAdjacencyMatrix() {
for (int i = 0; i < numVertices; i++) {
for (int j = 0; j < numVertices; j++) {
System.out.print
(adjacencyMatrix[i][j] + " ");
}
System.out.println();
}
}
// Sample usage
public static void main(String[] args) {
int numVertices = 4;
Graph graph = new Graph(numVertices);
graph.addEdge(0, 1, 1);
graph.addEdge(0, 2, 1);
graph.addEdge(1, 2, 1);
graph.addEdge(2, 3, 1);
graph.printAdjacencyMatrix();
}
}
Linked List Representation
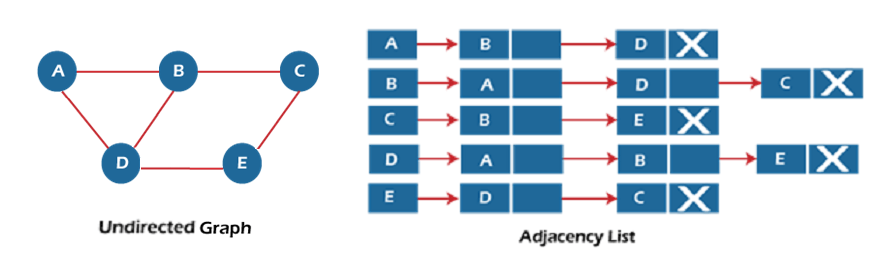
- In a linked list representation of a graph, each node of the linked list represents a vertex of the graph, and the edges are represented using linked lists.
- An adjacency list is a data structure used to represent a graph in the computer’s memory. It is a collection of unordered lists or arrays, one for each vertex in the graph
- Each list describes the set of neighbors of a particular vertex in the graph.
- This representation is efficient for sparse graphs, where the number of edges is much smaller than the number of possible connections between vertices
For example, consider a graph with vertices V1, V2, V3, and V4, where:
- V1 is connected to V2 and V4.
- V2 is connected to V1, V3, and V4.
- V3 is connected to V2 and V4.
- V4 is connected to V1, V2, and V3.
The adjacency list representation for this graph would be:
V1: V2, V4
V2: V1, V3, V4
V3: V2, V4
V4: V1, V2, V3
import java.util.LinkedList;
class Graph {
private int V; // Number of vertices
private LinkedList<Integer> adjListArray[];
// Constructor
Graph(int V) {
this.V = V;
adjListArray = new LinkedList[V];
for (int i = 0; i < V; i++) {
adjListArray[i] = new LinkedList<>();
}
}
// Function to add an edge to the graph
void addEdge(int src, int dest) {
adjListArray[src].add(dest);
adjListArray[dest].add(src);
// For an undirected graph
}
// Function to print the graph
void printGraph() {
for (int v = 0; v < V; v++) {
System.out.println
("Adjacency list of vertex " + v);
System.out.print("head");
for (Integer neighbor : adjListArray[v])
{
System.out.print(" -> " + neighbor);
}
System.out.println("\n");
}
}
public static void main(String args[]) {
int V = 5;
Graph graph = new Graph(V);
graph.addEdge(0, 1);
graph.addEdge(0, 4);
graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 3);
graph.addEdge(3, 4);
graph.printGraph();
}
}


