What Is A Priority Queue?
- A priority queue is an abstract data type that operates similarly to a regular queue, but with the added concept of each element having a priority associated with it.
- Elements in a priority queue are processed based on their priority, with higher priority elements being processed before lower priority elements.
- If two elements have the same priority, their order is determined by the order they were inserted into the queue.
In a priority queue, the key operations include:
- Insertion: Adding an element with a priority to the queue.
- Deletion: Removing the element with the highest priority from the queue.
- Peek: Viewing the element with the highest priority without removing it.
- Size: Determining the number of elements in the priority queue.
- isEmpty: Checking if the priority queue is empty.
Characteristics Of A Priority Queue
- Priority-Based Ordering: Elements are stored in the queue based on their associated priority. Elements with higher priority are processed before those with lower priority.
- Efficient Access to Highest Priority Element: A priority queue allows for efficient retrieval of the element with the highest (or lowest, depending on the implementation) priority, enabling quick access to the most critical element.
- No FIFO Ordering: Unlike a regular queue, a priority queue does not follow the First-In-First-Out (FIFO) principle. The order of retrieval is determined solely by the priorities of the elements.
- Dynamic Size Management: The size of a priority queue can change dynamically, depending on the number of elements and their associated priorities.
- Various Implementation Approaches: Priority queues can be implemented using different underlying data structures, such as binary heaps, binomial heaps, Fibonacci heaps, or even balanced binary search trees.
- Versatility: Priority queues find use in various applications, including task scheduling, network routing, graph algorithms, and simulation systems, where the management of elements based on their priorities is essential for efficient processing.
What Is Heap?
- In computer science, a heap is a specialized tree-based data structure that satisfies the heap property. Heaps are often implemented using arrays. They are a complete binary tree, meaning all levels of the tree are fully filled except possibly the last level, which is filled from left to right.
There Are Two Main Types Of Heaps
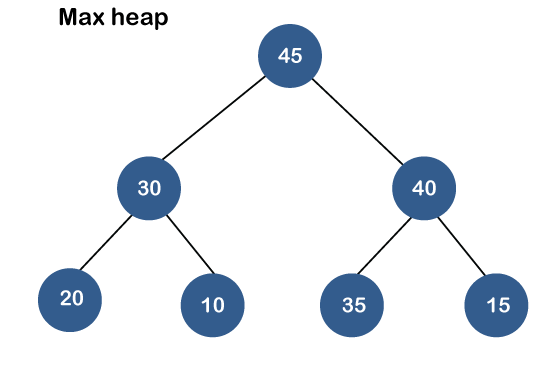
- Max-Heap: In a max-heap, for every node, the value of the node is greater than or equal to the values of its children. The largest element is at the root, and the same property applies to all subtrees.
- Min-Heap: In a min-heap, for every node, the value of the node is less than or equal to the values of its children. The smallest element is at the root, and the same property applies to all subtrees.
Applications Of Priority Queue
Priority queues find extensive applications in various domains due to their ability to manage and process elements based on their priorities. Some common applications of priority queues include:
- Operating Systems: Priority queues are used in operating systems for task scheduling, ensuring that processes with higher priority are executed before those with lower priority.
- Graph Algorithms: Algorithms such as Dijkstra’s algorithm and Prim’s algorithm use priority queues to efficiently process vertices or edges based on their priorities in graphs.
- Data Compression: Priority queues are utilized in Huffman coding, a popular lossless data compression algorithm, to assign shorter codes to frequently occurring symbols, improving the overall compression ratio.
- Networking: In networking applications, priority queues help manage network packets, ensuring that important or time-sensitive data is transmitted with higher priority than less critical data.
- Discrete Event Simulation: Priority queues are used to manage the events in simulations, ensuring that the events are processed based on their simulated time, allowing the simulation to proceed in the correct sequence.
import java.util.PriorityQueue;
public class PriorityQueueExample {
public static void main(String[] args) {
// Creating a priority queue of integers
PriorityQueue<Integer> priorityQueue
= new PriorityQueue<>();
// Adding elements with priorities
priorityQueue.add(30);
priorityQueue.add(20);
priorityQueue.add(40);
priorityQueue.add(10);
System.out.println("Priority Queue elements:
" + priorityQueue);
// Removing elements based on priority
while (!priorityQueue.isEmpty()) {
int element = priorityQueue.poll();
System.out.println
("Processing element with priority: " + element);
}
}
}


