Overview
- Basics of function
- Measuring Algorithm Performance
- Why analysis is required
- Types of algorithm analysis
- Time complexity
- Asymptotic Analysis
- Asymptotic Notations
- Calculation Big 0 notation
Basic Of Functions
T = f(n) [ y = f(x) ]
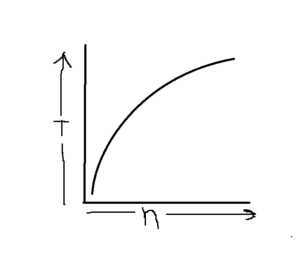
Measuring Performance Of Algorithms
Algorithm analysis is an important part of computational complexity theory, which provides theoretical estimate’mfor the required resources of an algorithm to solve a specific computational problem
It is the determination of the amount of time and space resources required to execute it .
It is the determination of the amount of time and space resources required to execute it .
Why Analysis Is Required?
Types of Algorithm Analysis
1) Best case
2) Worst case
3) Average case
Certain input takes less time for an algorithm to accomplish its task .This is best case
Certain input takes Max time for an algorithm to accomplish its task .This is worst case
All other cases /total no.of cases = Average case
2) Worst case
3) Average case
Time Complexity
It is a measure of rate of change in time with respect to change in input size
Various asymptotic notations are there to represent time complexity of an algorithm.
Asymptotic Analysis
we donot calculate the actual time taken by the algorithm to solve the problem, rather we are interested in how the time taken by an algorithm increases with the input size
Asymptotic Notation
1) Big O Notation
provides an upper bound on the growth rate of time . It represent the worst case scenario
2) Omega Notation
provides a lower bound on the growth rate of time. It represents the best case scenario
3) Theta Notation
provides both an upperbound and lowerbound on the growth rate of time. It represents the average case scenario .
provides an upper bound on the growth rate of time . It represent the worst case scenario
2) Omega Notation
provides a lower bound on the growth rate of time. It represents the best case scenario
3) Theta Notation
provides both an upperbound and lowerbound on the growth rate of time. It represents the average case scenario .
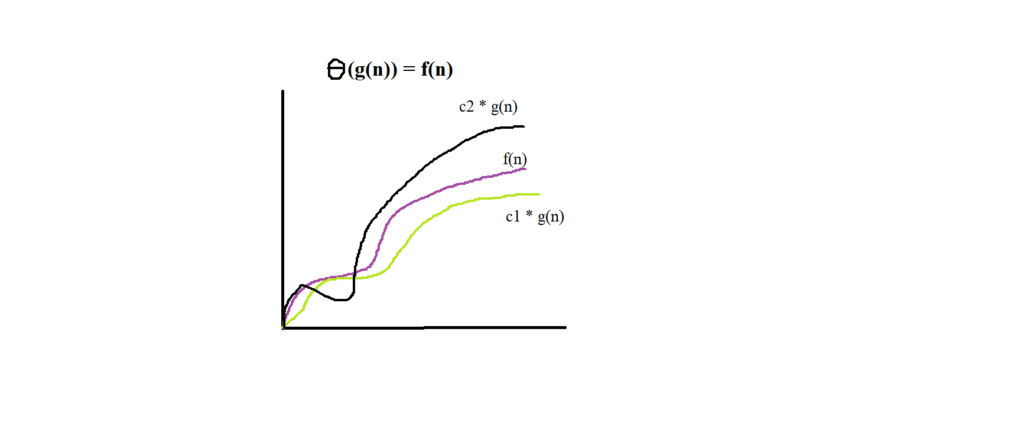
c1 * g(n) <= f(n) <= c2 * g(n)
here, c1 and c2 are positive constant
for all n >= n0
if g(n) = 3n3 + 5n2 + 4
then
g(n) = n3
for some no such that n>=n0
if g(n) = 3n3 + 5n2 + 4
then
g(n) = n3
for some no such that n>=n0
Big O Notation
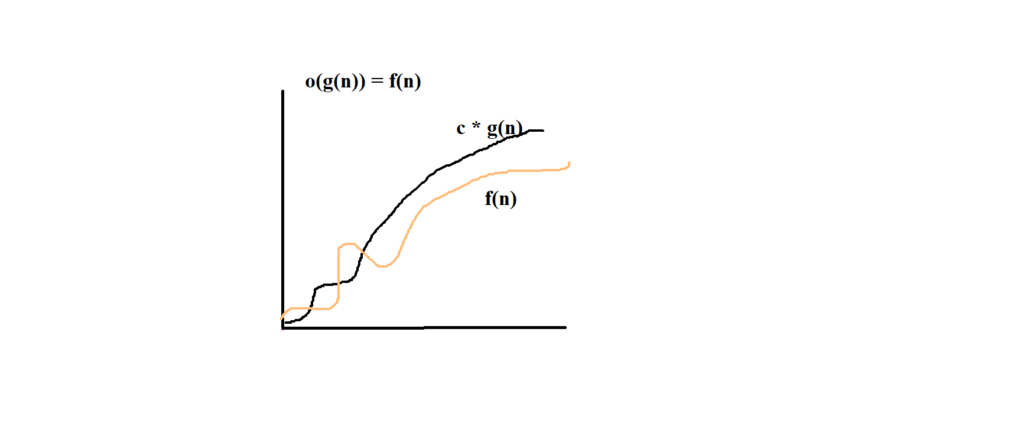
O <= f(n) <= g(n)
for all n >= n0
Omega Notation
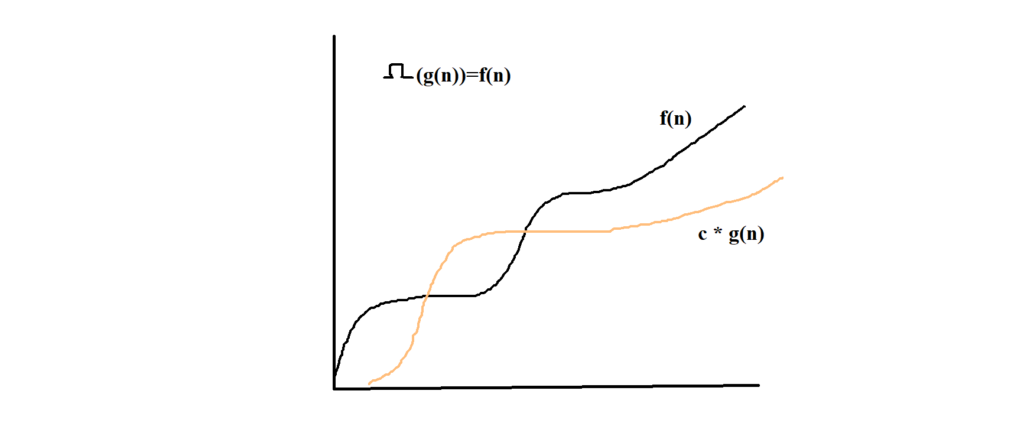
c * g(n) <= f(n)
for all n >= n0
Calculate O(n)
1) Factorial
2) Insertion Sort
f=1
for i=1 to n
f=f*i;
for(i=1 to n)
temp=A[i]
for(j=i-1 to 0)
if(A[j]>temp)
A[j+1]=A[j];
else
break;
A[j+1]=temp;
o(1) o(log n) o(n) o(n logn)
o(n2) o(n2log n) o(n3)
o(a4)


