Overview
2) Adjacent nodes
3) Degree of anode
4) Path
5) Connected Graph
6) Labelled & Weighted Graph
7) Multi Graph &-Directed Graph
8) Complete Graph
9) Representation of Graph
What Is Graph?
- Graph is nonlinear data structure
- Graphs are a fundamental data structure used in computer science and mathematics to represent relationships between different entities. They consist of a set of vertices or nodes, connected by edges or links.
- These vertices can represent any discrete object or entity, while the edges depict the relationships or connections between them.
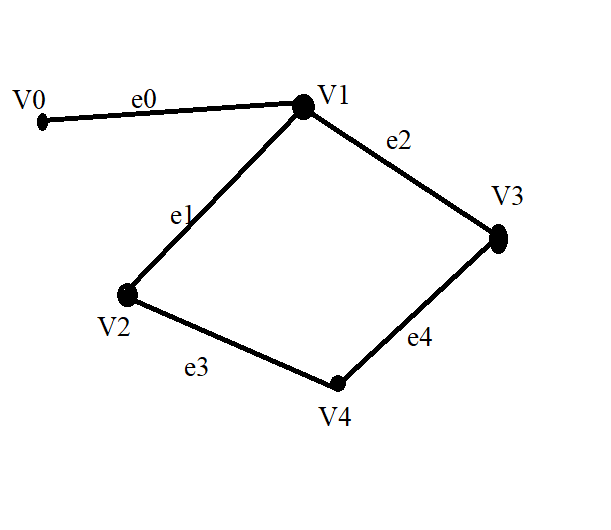
e0 = [V0, V1]
e1 = [v1, v2 ]
V = {V0, V1, V2, V3, V4 }
E = {e0, e1, e2, e3, e4}
A Graph Consists of two things
A set V of elements called nodes.
A set E of edges such that each edge e in E is identified with a unique (unordered)
pair [u ,v] of nodes in V, denoted by e = [u,v] we indicate the parts of the graph by writing G=(V,E)
Some Common Types Include
- Directed and Undirected Graphs: In directed graphs, the edges have a specific direction, while in undirected graphs, the edges have no direction.
- Weighted and Unweighted Graphs: Weighted graphs assign a weight or cost to each edge, whereas unweighted graphs do not.
- Cyclic and Acyclic Graphs: Cyclic graphs contain cycles, which are paths that lead back to the starting node, while acyclic graphs do not have any cycles.
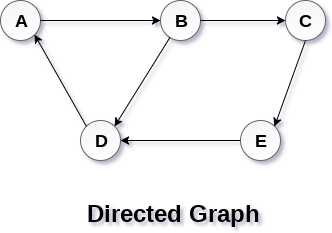
Directed & Undirected Graph
Undirected Graphs:
- In an undirected graph, the edges have no specific direction associated with them.
- They represent symmetric relationships. For example, if there is an edge between nodes A and B, it implies that there is a symmetric relationship between A and B; you can traverse from A to B and vice versa.
- Formally, an edge {A, B} in an undirected graph indicates a connection between node A and node B, without any notion of a one-way relationship.
Directed Graphs:
- In a directed graph (also known as a digraph), each edge has a specific direction associated with it.
- They represent asymmetric relationships. For example, if there is a directed edge from node A to node B, it implies a one-way relationship or a specific direction from A to B.
- Formally, an edge (A, B) in a directed graph indicates a directed connection from node A to node B.
Adjacent Nodes
If e = [u,v] then u and v
are called adjacent nodes or neighbors .
Degree Of Node
If deg(u)=0, then u is called isolated node
Path
p =(v0, v1, v2,…… vn)
The path is said to be closed if v0 =vn
Simple & Complex Path
Connected Graph
A graph is said to be connected if there is a path between any two of its nodes
Tree Graph
A connected graph T without any cycles is called a tree graph or free tree, or simply a tree
This means in particular, that there is a unique simple path P between any two nodes u and v.
Labelled Graph
A graph is to be labelled if its edges are assigned data.
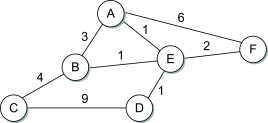
Weighted Graph
A graph G is said to be weighted if each edge e in G is assigned a non-negative numerical value W(e)
called the weight or length of e
Multiple Edge
Distinct edges e and e’ are called multiple edges if they connect the same end points that is ,
if e = [u,v] and e’ = [u ,v]
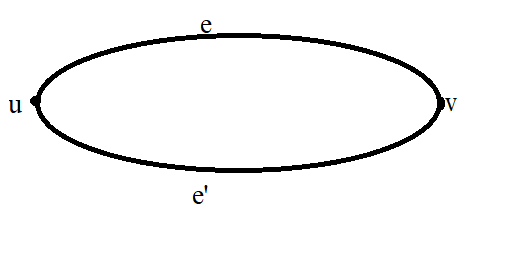
Loop
An edge is called loop if it has identical end points.
IPv4 – 32 Bits
IP v6- 128 Bits
Multi Graph
Multi Graph is a graph consisting of multiple edges and loops
Directed Graph
A directed graph G also called digraph in same as multigraph except that
each edge e is assigned a direction
e = (u,v)
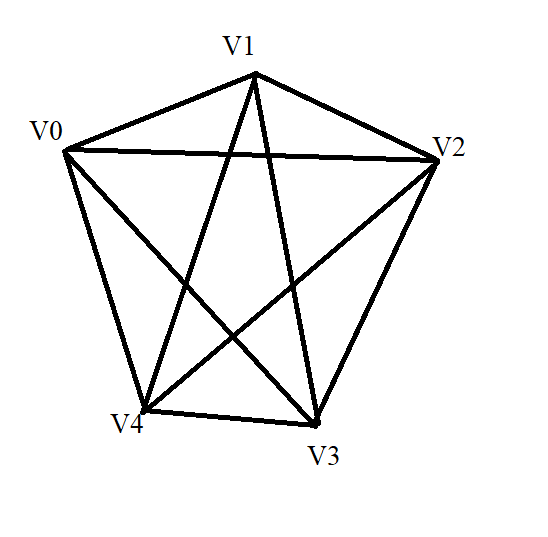
Complete Graph
A simple graph in which there exists an edge between every pair of vertices is called a complete graph.
It is also known as a universal graph or clique
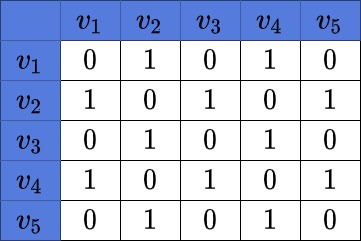
- Adjacency Matrix Representation
- List Representation
Suppose G is a simple graph with m nodes, and suppose the nodes of G have been ordered and are called v1, v2, v3 ………..Vm. Then the adjacency matrix A= (aij) of the graph G is the mxm matrix defined as
1 – v1 is adjacent to vj
0 – otherwise
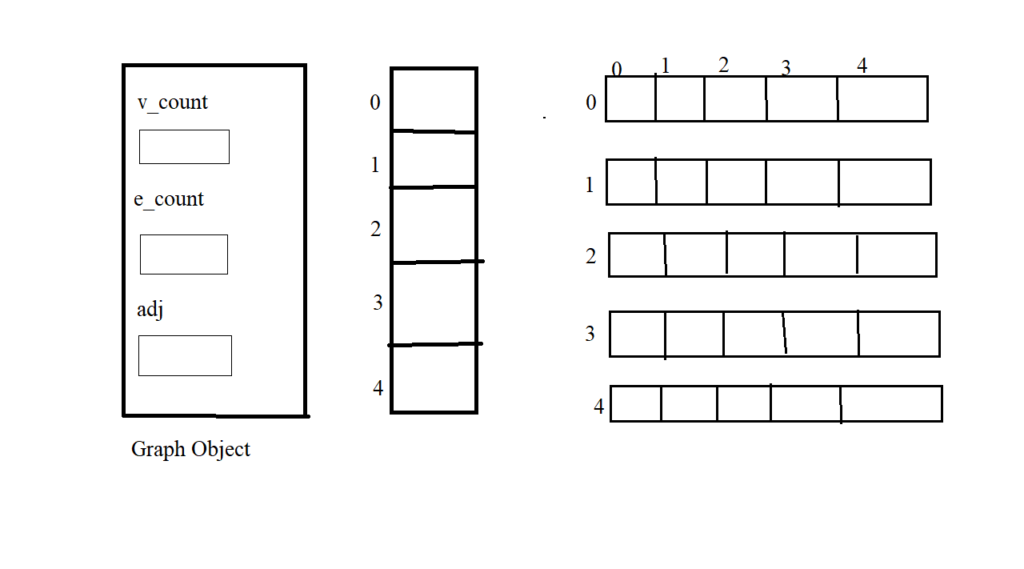
The graph is stored as a linked structure. The adjacency list stores information about only those edges that exists. The adjacency list contains a directory and a set of linked lists.
The directory contains one entry for each node of the graph. Each entry in the directory points to a linked list that represents the nodes that are connected to that node Each node of the linked list has three fields , one is node identifier , second is the link to the next field and the third is an optional weight field which contains the weights of the edges
int vertex;
Node next;
}
class graph{
private int v-count;
private Adj List arr;
}
class AdList{
private node stand
}