Overview
- Complete Binary Tree
- Almost Complete Binary Tree
- Heap
- Insertion in heap
- Deletion in heap
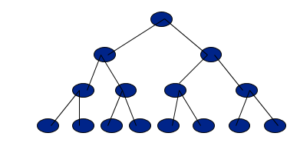
Complete Binary Tree
- All level must be completely fill
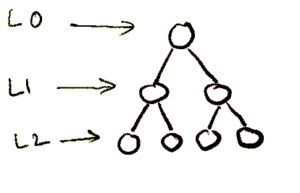
Almost Complete Binary Tree
- All level must be completely filled except possibly the last level and all the node in the last level must be left aligned
Heap
- Heap is a data structure
- Heap is used in a sorting algorithm known as heap sort
- Heap are of two types 1) Max Heap (Default )
2) Min Heap
Heap Properties
The value at node N is greater than
or equal to value at each children of Node N
- Heap Must be almost binary tree
- no ≥ n1 , and no ≥ n2
This heap is Max heap
Example:
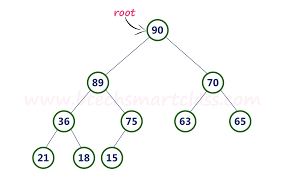
Representation Of Heap
- Unless otherwise stated ,heap is maintained in memory by a linear array
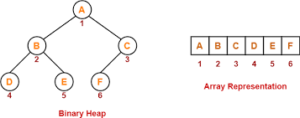
How To Find Parent Or Child Node?

How to find index of child nodes?
- index is index of node N index of left child = 2 * index +1 index of right child = 2* index -12
How to find index of parent node?
- index of node N = index
index of Parentnode of N =(index-1)/2
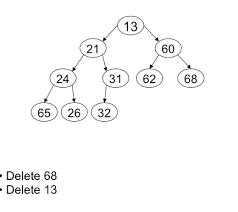
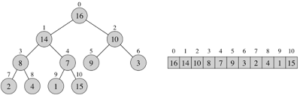
Insertion
Deletion
- Root node can only be deleted